ACORDEON DIGITAL_YESENIA FLORES ROMERO
Monomios y Polinomios:
SUMA: En la suma de
monomios y polinomios, el objetivo es la reducción de términos semejantes. Será
importante el tener presente, que dos expresiones algebraicas con signos
iguales, se deben de sumar no importando su signo y su resultado adquiere el
signo único que presenta el ejercicio. Si ambos sumandos son positivos el
resultado será positivo, si ambos sumandos son negativos el resultado será
negativo.
En caso contrario si dos
expresiones algebraicas tienen signos diferentes, se debe de restar. A la
expresión mayor en términos absolutos, se le resta la menor y el resultado
adquiere el signo de la expresión con mayor valor absoluto.
Ejemplo:
RESTA: Para
restar monomios es necesario que sean semejantes. Monomios semejantes son aquellos que tienen la misma parte
literal y el mismo grado.
Se restan monomios semejantes,
sumando al minuendo el opuesto de cada término semejante del sustraendo.
La resta de monomios es muy parecida a la suma, sólo que hay que cambiar los números del sustraendo por su
simétrico y se resuelve aplicando las reglas de la suma.
Ahora bien, si tomamos en cuenta que el valor absoluto de un número algebraico es el valor de dicho número sin tener en cuenta su signo.
MULTIPLICACIÓN DE MONOMIOS: Se
multiplican los coeficientes y se aplica la ley de los signos.
En seguida, se multiplican las
literales, si son iguales se suman sus exponentes y si son diferentes se queda
expresada la multiplicación.
Finalmente se coloca el
producto de las literales después del producto de los coeficientes.
De un monomio por
un polinomio: se
multiplica el monomio por cada término del polinomio, siguiendo las mismas reglas
anteriores.
El resultado esta formado por el mismo número de término que tenga el polinomio factor, ademas es conveniente ordenar el resultado.
El resultado esta formado por el mismo número de término que tenga el polinomio factor, ademas es conveniente ordenar el resultado.
DIVISIÓN DE MONOMIOS:
Para dividir dos monomios debemos seguir los siguientes pasos:
(15x2) / (3x)=
- Dividir los coeficientes. 15: 3=5
- Dividir la parte literal (las letras que aparecen en los monomios).
De esta modo, (15x2) / (5x)= 3x
Ejemplos:
8 a / 2 a = (8/2).(a/a)= 4
15 ay /3a = (15/3) (a.y)/ a = 5 y
12 bxy / -2 bxy = (12/-2) (b.x.y)/(bxy.) = -6
-6 v2 . c. x/-3vc= (-6/-3) (v2 .c. x) /(v. c) = 2 v
DIVISIÓN DE UN POLINOMIO POR UN MONOMIO
La división de un polinomio por un monomio (sólo si es posible) se obtiene dividiendo cada término del polinomio por el monomio, obteniendo como resultado otro polinomio.
Ejemplo:
QUÍMICA
Ejemplos de estructuras de los compuestos orgánicos
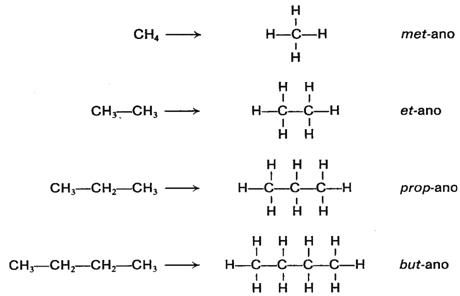
INGLES
Partes de una oracion:
Verbos Regulres e Irregulares
LOGICA
TIPOS DE ARGUMENTOS
Argumento deductivo:
Un argumento deductivo es aquel cuya conclusión deriva de manera necesaria de sus premisas, a esta propiedad exclusiva de este tipo de argumento se le denomina validez.
En un argumento deductivo la inferencia3 es más fuerte que en los argumentos inductivos. Esto se debe a que el contenido informativo de la conclusión está ya en las premisas, es decir, en la conclusión no se obtiene información nueva. La conclusión sólo hace explícito algo que ya se dice en las premisas, aunque de una manera implícita. Veamos el siguiente ejemplo:
• Todos los gatos maúllan
• Félix es un gato
- Félix maúlla
Razonamiento Inductivo
Un razonamiento inductivo, por lo tanto, consiste en considerar varias experiencias individuales para extraer de ellas un principio más amplio y general. Es importante tener en cuenta que, pese a que se parta de premisas verdaderas, la conclusión puede resultar falsa. Que un razonamiento inductivo derive en una conclusión verdadera es apenas una probabilidad, cuyo grado varía de acuerdo al número de premisas que se consideren y a las características de éstas.
Un argumento analógico o argumento comparativo es la forma más simple y comúnmente utilizada de razonamiento inductivo. Se fundamenta en la similitud de dos elementos para concluir que otro elemento –cuyas características son similares a las de estos dos elementos- puede también ser similares a estos.
Argumento Abductivo
Un argumento abductivo se refiere a dos conceptos que se relacionan entre sí, pero aun así son diferentes. Ambos se refieren a argumentos explicativos.
El primer sentido se refiere a la parte de un argumento en el que se genera la hipótesis, mientras que el segundo sentido se refiere a la parte del argumento en el que se justifica la hipótesis.
El primer sentido que se mencionó era popular anteriormente, pero, en la actualidad, ha caído en desuso, por lo que prevalece el segundo sentido. Este segundo sentido es llamado generalmente “inferencia sobre la mejor explicación”.
Algunos filósofos señalan que el argumento abductivo es uno de los tipos de inferencia que se usa de manera más frecuente, tanto en la vida diaria como en el marco del razonamiento científico.
No existe un modelo específico para los argumentos, lo que genera argumentos entre los pensadores. Sin embargo, lo más común es que se presenten dos premisas y una conclusión que es la mejor explicación para estas dos premisas.
Cabe destacar que los argumentos abductivos no ofrecen un razonamiento realmente lógico, sino que ofrecen la mejor explicación dado las premisas.
Argumento probabilístico
Cualquier argumento que implica la teoría de probabilidades, se llama argumento probabilístico. Estos argumentos se apoyan en la probabilidad de que ocurra algún evento. En este caso se utilizan muestran que auxilian a la conclusión.
Algunos casos del uso de la probabilidad son:
Sorteos, juegos de azar, estimación de parámetros de la población, estudio de sucesos inciertos, cuantificar los resultados de experimentos aleatorios, etc.
Argumento de autoridad
Es un argumento inductivo. A pesar de que ciertas clases de argumentos de autoridad pueden constituir fuertes argumentos inductivos, muchas veces la apelación a la autoridad se aplica a menudo falaz: ser la autoridad no significa ser un experto, o no hay consenso entre los expertos en la materia, o ambas cosas.
Ejemplo:
Premisa 1: De acuerdo a la ciencia médica, no hay vida después de la muerte.
Premisa 2: La ciencia médica esta bien establecida.
Conclusión: Está claro que no hay vida después de la muerte.
Argumento conductivos
Es un argumento no deductivo donde se tiene una serie de consideraciones positivas y negativas para equilibrar.
Para la evaluación de los argumentos conductivos:
- Determina, si las premisas ofrecidas para apoyar la conclusión son aceptables.
- Define, si las premisas ofrecidas para apoyar la conclusión positiva son relevantes para la misma, y evalúa la solidez de las razones.
- Establece, si las contra consideraciones reconocidas por el argumentador son negativamente relevantes para la conclusión.
- Piensa, si las contra consideraciones adicionales, no reconocidas por el argumentador, son negativamente relevantes para la conclusión.
- Reflexiona sobre si las premisas, en su conjunto, supera las contra consideraciones, en su conjunto, y haz un juicio.
TIPOS DE FALACIAS
GENERALIZACIÓN APRESURADA
GENERALIZACIÓN APRESURADA
En lógica, la generalización apresurada, muestra sesgada o Secundum quid,es una falacia que se comete al inferir una conclusión general a partir de una prueba insuficiente. Una generalización apresurada puede dar lugar a una mala inducción y por tanto a una conclusión errónea. Por ejemplo, considérese el siguiente argumento:
- Juan es alto y es rápido.
- María es alta y es rápida.
- Matias es alto y es rápido.
- Por lo tanto, todas las personas altas son rápidas.
Concluir que todas las personas altas son rápidas, porque haya tres que lo sean, es una generalización apresurada. Es muy probable que haya personas que sean altas y que sin embargo no sean rápidas.
El límite entre una generalización apresurada y una buena inducción a veces puede ser difuso, y establecer un criterio claro para distinguirlos es pare del problema de la inducción.
Falsa analogía
La falacia de falsa analogía ocurre cuando un escritor o un comunicador usa una analogía que hace una comparación pobre entre dos cosas con el fin de ilustrar un concepto o una idea. Las analogías concisas frecuentemente se usan con éxito para ilustrar conceptos complicados o una parte específica de un tema controversial. Sin embargo, las analogías falsas por lo regular se usan, ya sea de manera intencional o sin intenciones, para apoyar ideas que tienen argumentos pobres o carecen de evidencia.
Ad Misericordiam
El argumento Ad Misericordiam es la apelación a la piedad para lograr convencimiento cuando se carece de argumentos. Es una falacia que consiste en la manipulación de los sentimientos para evitar un castigo.
Un buen ejemplo sería: “Señor policía, me pasé el semáforo en rojo porque estoy apurado. Tengo a mi madre internada y debo llevar las órdenes al sanatorio para que la puedan operar. Por favor, no me multe”.
Hipótesis contraria a los hechos
Si yo nunca hubiera aparecido, tu nunca habrias aprendido nada acerca de las falacias
Dictor Simpliciter
Quiero decir que esto es solo una materia de clases y tu sabes que las cosas se aprenden en la escuela y no tienen nada que ver con la vida.
Envenenar el pozo
"No puedes irte con el,Polly, es un mentiroso un tramposo, es una rata."
La seguridad informática, también conocida como ciberseguridad o seguridad de tecnologías de la información, es el área relacionada con la informática y la telemática que se enfoca en la protección de la infraestructura computacional y todo lo relacionado con esta y, especialmente, la información contenida en una computadora o circulante a través de las redes de computadoras.1 Para ello existen una serie de estándares, protocolos, métodos, reglas, herramientas y leyes concebidas para minimizar los posibles riesgos a la infraestructura o a la información. La ciberseguridad comprende software (bases de datos, metadatos, archivos), hardware, redes de computadoras y todo lo que la organización valore y signifique un riesgo si esta información confidencial llega a manos de otras personas, convirtiéndose, por ejemplo, en información privilegiada.
La definición de seguridad de la información no debe ser confundida con la de «seguridad informática», ya que esta última solo se encarga de la seguridad en el medio informático, pero la información puede encontrarse en diferentes medios o formas, y no solo en medios informáticos.
La seguridad informática es la disciplina que se encarga de diseñar las normas, procedimientos, métodos y técnicas destinados a conseguir un sistema de información seguro y confiable.
Puesto simple, la seguridad en un ambiente de red es la habilidad de identificar y eliminar vulnerabilidades. Una definición general de seguridad debe también poner atención a la necesidad de salvaguardar la ventaja organizacional, incluyendo información y equipos físicos, tales como los mismos computadores. Nadie a cargo de seguridad debe determinar quién y cuándo puede tomar acciones apropiadas sobre un ítem en específico. Cuando se trata de la seguridad de una compañía, lo que es apropiado varía de organización en organización. Independientemente, cualquier compañía con una red debe tener una política de seguridad que se dirija a la conveniencia y la coordinación.
Identidad digital
Identidad 2.0, también llamada identidad digital, es la revolución anticipada de la verificación de la identidad en línea utilizando tecnologías emergentes centradas al usuario tales como el estándar OpenID o Microsoft Windows CardSpace. Se encuentra dentro de la teoría de la Web 2.0, donde enfatiza en un modo simple y abierto método de identificación en transacciones cuyo proceso es similar al mundo real, como por ejemplo una licencia de conducir.
Según Aparici, R. y Osuna Acedo, S. (2013) Identidad 2.0 o identidad digital es todo lo que manifestamos en el ciberespacio e incluye tanto nuestras actuaciones como la forma en la que nos perciben los demás en la red”.1
Todas nuestras actuaciones dentro del espacio digital (imágenes, comentarios, links visitados, lugares donde publicamos nuestros datos, etc.) conforman nuestra identidad o perfil digital. Por tanto es imprescindible tener en cuenta que a través de esto los demás nos verán de un modo u otro en el ciberespacio.
Una de las competencias personales necesarias en la sociedad actual para el ciudadano digital es el saber gestionar su propia identidad digital, actuando de una manera ética y legal dentro de una correcta cultura de la participación.
Aparici, R. y Osuna Acedo, S. (2013), argumentan que “para gestionar la identidad digital se hace necesario gestionar los siguientes elementos: visibilidad, posicionamiento web, reputación y privacidad en internet”
Se pueden crear diferentes identidades de un mismo individuo en Internet y además la identidad digital que una persona se crea no tiene porqué coincidir con la identidad analógica de esa persona, con sus características en el espacio físico.
Pero, hay quien no tiene acceso a participar en la cultura digital y por tanto a la gestión de su identidad en el ciberespacio creándose así una brecha digital y una exclusión social de dichas personas.
MI PLAN DE VIDA
Mi nombre es Yesenia
Flores Romero, soy una joven de 15 años actualmente, actualmente estoy cursando
el primer semestre de preparatoria en el
CBTis 229 y este es mi plan de vida
Una de mis fortalezas
como persona es que soy una buena alumna, durante mis 12 años de preparación
escolar he mostrado un buen comportamiento y buena actitud, ganándome así
varios reconocimientos y aprecio de mis anteriores maestros.
Soy una persona muy
comprensiva, me gusta ayudar. Otra de mis fortalezas que yo poseo es que
aprendo rápido, al igual que no soy conformista, es decir, yo busco muchas más
oportunidades de las que tengo, y hago lo posible por salir adelante a pesar de
cada mala situación que se me presente.
Soy una persona
divertida, y entendible.
Pero no todo es lado positivo
en mí, con esto me refiero es que tengo ciertas debilidades que me perjudican
como persona en el ámbito social y familiar
Una de mis debilidades
es que hay momentos en los que soy muy floja, ya sea para hacer alguna tarea, o
practicar un deporte.
Otra seria que hablo de
mas, oh digo cosas sin sentido perjudicando a terceras personas, al igual que
no soporto comentarios negativos y me tomo las cosas malas muy en serio,
provocando a base de eso que me sienta mal y me dé por vencida.
Otra debilidad que
tengo es que digo malas palabras inclusive en lugares que novan, pero soy
honesta y lo acepto, se oye mal.
Tengo muchos defectos
como cualquier persona pero es ahí cuando debo de portarme más fuerte, más
justa, más responsable y tratar de quitar eso.
Me he puesto a pensar
que si no cambio mi actitud negativa no llegare muy lejos, al contrario, se va
debilitando mis fortalezas, y mis metas se pueden venir abajo con todo lo
propuesto que tengo, así que como ya mencione anteriormente, debo salir
adelante ahora más que nunca.
Me he propuesto a
terminar una carrera, tal vez estudiare Contaduría o Derecho, pero aun no tengo
bien decidido eso, pero lo que sí es seguro es que si conseguiré un título
profesional, podre sacar adelante a mi familia, tener una casa propia, quizá un
auto, un buen trabajo y quizá una familia propia.
Mis principales valores
son los siguientes:
Mi familia: Mi conducta o valor apuesto a esto
es la separación, el egoísmo, la falta de respeto. Esto perjudica mucho nuestra
convivencia y puedo llegar a tener dificultades.
Por lo que
voy hacer todo lo posible por mantener a mi familia unida, tomando una actitud
positiva, obedeciendo, provocando así la mejora de la estabilidad familiar.
Los amigos: Valor opuesto es la enemistad, algo
que hace que las personas se alejen.
Para vencer
esto será necesario ser sincera, apoyarlos, comprender, ser una persona en la
cual se puede confiar, pero es importante saber cómo son el tipo de personas
con las que convivo.
El amor: El valor opuesto al amor es el odio,
provoca la distancia y una mala imagen de mi persona.
Este mal
valor lo venceré dando una buena idea sobre mí, amar a mis personas queridas
como se debe, respetar, confiar, ayudar, entender, querer.
El respeto: Valor opuesto de este es la falta
de respeto, la ignorancia, el egoísmo. Vivimos en una sociedad en la cual este
valor ya no le tiene importancia, al contrario, es el más opacado de todos a
pesar de que es el principal y la base de los demás.
Para poder
vencer todo eso es necesario que yo lo practique para todo, esto incluye en
todos los ámbitos sociales, tomando consideración de este en todas las
personas.
MI
VISION
Lo que yo veo en un
futuro es grande, pues quiero progresar y obtener una buena vida, ya mencione
anteriormente que quiero un buen trabajo, una casa, una familia, un auto quizá.
Quiero tener un buen futuro.
MI
MISION.
Mi misión es lógralo,
lograr mis metas, mis sueños, mis visiones, mis expectativas. Pondré mucho
empeño en las etapas que aún me faltan, para así alcanzar la victoria y
sentirme bien con todo mi esfuerzo.
MI
META EN EL ASPECTO ESPIRITUAL
ü Una meta en
el aspecto espiritual es seguir siendo creyente de una religión o inclusive
poder hacer un servicio a la comunidad religiosa, es decir, ser misionera, ser
lectora o esas cosas.
ü Otra podría
ser alimentar mi espíritu haciendo alguna actividad tranquila; practicar yoga
tal vez, todo estopara mantenerme tranquila conmigo misma.
En el primer aspecto no
lo tengo del todo bien definido ya que hay veces en las que no soy tan
creyente.
Pero me propongo hacer
el intento para hacer algún servicio religioso.
Esto lo lograre
aproximadamente el 15 de Enero de 2018, tendrá beneficios para la sociedad
espiritual y también para mí.
Pero vuelvo a repetir
nuevamente, esto no es nada seguro dependiendo de mis creencias que tenga
posteriormente, pero respetare la de los demás alejándome de críticas o
prejuicios.
Esto lo lograre
evitando los malos comentarios, tomando el valor de respeto como el principal y
dejar los prejuicios de un lado, además de la paz interior en mí.
MI
META PRIORITARIA EN EL ASPECTO
INTELECTUAL
Una de mis metas en
este aspecto es:
ü Terminar una
profesión, ya mencionado anteriormente aun no tengo bien definido qué carrera elegiré,
pero dado caso que sea contaduría, es necesario saber cómo lo hare, es por ello
que lo describo a continuación.
Al terminar mis
estudios universitarios buscare un trabajo, ya sea como ayudante en un despacho
contable, para iniciar así una pequeña practica para después poder conseguir
uno mejor pagado ya sea en una empresa grande o como contadora privada de
distintas personas, pues he escuchado que es un buen trabajo.
Estamos a 19 de
septiembre de 2017, para el día 20 de Septiembre de 2024 ya estaré consiguiendo
algún trabajo como auxiliar contable aproximadamente. Sera hasta 1 o 2 años muy
máximos ya poder contar con un trabajo estable en una empresa.
Tendré un buen sueldo,
y podre empezar ahorrar para mis gastos posteriores que tenga
Seré reconocida como
una buena contadora y solicitada por varios clientes, logrando así otro merito
ganado
Los valores que tendré
para logar esto serán la perseverancia, su mala actitud de este es rendirse,
pues como dicen ``El que persevera alcanza``
Otro valor será el
respeto, como ya mencione anteriormente, es la base de todo.
El conocimiento, al
igual que la responsabilidad, pues ser contador no es nada fácil
Todos los valores no se
verán opacados si tomo iniciativa y buena actitud de mi parte.
MI
META PRIORITARIA EN EL ASPECTO AFECTIVO/ EMOCIONAL
ü Mi meta
prioritaria en este aspecto es poder formar una familia y casarme al concluir
mis estudios universitarios, posteriormente formar una familia, seguir teniendo
buenas compañías.
Para esto será
necesario de una vez pensar en lo que hare.
Al terminar mis
estudios o mi carrera, buscare un trabajo como ya mencione anteriormente, ya
que tenga todo esto decidiré por encontrar una buena persona con la cual
compartir lo que resta de mi vida.
20 de septiembre de
2017, estoy cursando el primer semestre de nivel media superior, será hasta el día
22 de Diciembre de 2027 aproximadamente cuando me casare, pero todo esto depende
de lo que pueda pasar posteriormente, ya que no es fácil encontrar una buena
persona que comparta gustos en común.
Antes de la unión
matrimonial, comenzare a ahorrar junto a mi pareja para los preparativos, para
poder empezar a construir una vivienda y para tener recursos con los cuales
poder vivir bien.
Ya que tengamos todo
esto tal vez tengamos 2 hijos, estos les brindaremos todos los recursos
necesarios para su sano crecimiento.
Viviremos bien, ya que
ambos nos apoyaremos mutuamente.
Mi
principal valor para logara esto será el amor, la comprensión, y la unión.
Tendremos antivalores como son el odio, la separación. Para poder combatir esto
debo dar lo mejor de mí y apoyare a mi
familia y pareja en lo que pueda, siempre cuidándolos y dándonos ánimos para
cada situación difícil.
MI META PRIORITARIA EN EL ASPECTO FAMILIAR
MI META PRIORITARIA EN EL ASPECTO FAMILIAR
ü Una de mis
metas prioritarias en el aspecto familiar es poder brindarles a mi familia
actual más recursos, terminar su casa, darles más atención y poder
fortalecernos.
Esto no será nada
sencillo, pues todo esto depende de que yo consiga un buen trabajo. Para poder
regresarles todo el esfuerzo que han hecho por mis durante mis primeros años de
preparación escolar.
Si empiezo a trabajar
desde ahora 25 de septiembre de 2017, y ahorrar más y más, no solo para mis
estudios sino también para ayudar a mi familia, a más tardar el 25 de Enero del
2022 empezare con terminar mi casa.
Después de esto, al
obtener un buen salario empresarial le daré a mis padres un descanso, darles más
recursos médicos y ocuparme de darles varias atenciones.
Mis principales valores
para lograr esto serán la familia, la perseverancia, la unión, el amor.
Alguna de las malas
actitudes que pueda haber, puede ser la falta de comunicación entre familia, ya
que puede ocasionar muchos conflictos, pero para ello, no debo enojarme ni
desobedecer, si no hacer que la convivencia mejore junto a ella el cariño.
MI
META PRIORITARIA EN EL ASPECTO RECREATIVO
ü En este
aspecto mi principal meta es poder divertirme de una manera sana, a que me
refiero con esto, que mi deporte favorito es el futbol, por ello una buena
manera de divertirme es pertenecer a un equipo femenil de futbol por un tiempo,
o inclusivamente, cuando tenga mi familia poder jugar con ellos.
Actualmente no practico
el deporte por la falta de tiempo e igual de recursos, pero si me sigo
esforzando como lo he estado haciendo, empezare mis entrenamientos el próximo
semestre.
Ya que empiece desde
cero a practicar lo más probable es que aproximadamente 22 de Enero de 2019 ya estaré
más preparada en este deporte.
Pero podre divertirme
al practicar en cada sesión deportiva de una manera sana, mas sin embargo si me
gustaría poder participar en un equipo femenil.
Los valores para poder
llevar a cabo esto serán la diversión sana, el deporte, la responsabilidad, el
entusiasmo, la perseverancia.
Algunos de ellos se
verán opacados por la irresponsabilidad, el cansancio, el estrés, o quizá la
falta de compromiso, por ello, debo de pensar bien las cosas antes de
realizarlas, por lo que me comprometeré a echarle ganas, divertirme bien por
supuesto, ser activa y respetuosa.
Al concentrarme en mi y
en mi integridad física, esta es una buena manera de divertirse y no solo salir
con amigos a un antro o disco, pues nos exponemos más a las malas influencias
vicios.
MI
META PRIORITARIA EN EL ASPECTO SOCIAL
ü Mi meta
prioritaria en este aspecto es poder seguir teniendo una buena convivencia con
amigos, familiares y entre toda la sociedad.
ü Otra meta
prioritaria es poder ayudar a la sociedad de hoy en día en diferentes factores,
pues hemos pasado por situaciones difíciles que sería bueno brindar apoyo a los
más necesitados, por ello quiero ya sea poder donar víveres, brindar ayuda personal,
haciendo servicios sociales, entre otros.
Quiero tener buenas
compañías durante toda mi vida, seguir conviviendo con anteriores compañeros
que comparten algunos gustos comunes conmigo, al igual que poder tener una
buena relación con mi pareja, con mis familiares y diferentes personas que me
rodean.
En un futuro tal vez me
anime a ser rescatista, o tener la oportunidad de donar diferentes artículos.
También me gustaría
crear muchas campañas que concienticen a las personas sobre la contaminación
del planeta, ya que por la ignorancia no se han dado cuenta de los daños que
nosotros mismos le ocasionamos.
Mis valores que tendré
presente durante este reto será la solidaridad, el respeto, la unión, la paz,
la equidad para todos.
Debo combatir todos los
prejuicios que la sociedad ha de tener, y esquivar algunas barreras que quizá
el mundo político forme.
MI
META PRIORITARIA EN EL ASPECTO CORPORAL
ü Mi meta que
tengo para este aspecto, tal vez pueda sonar muy soberbio, pero me gustaría
ejercitarme teniendo así una vida sana y una buena figura, al igual que una
excelente condición física.
Si empiezo a
ejercitarme correctamente desde esta semana, será el día 25 de septiembre de
2017, posiblemente alcance una mayor rendición en 3 o 4 meses después, es
decir, esto sería por Diciembre o Enero de 2018.
Si continúo
ejercitándome día a día, sanamente, y practicar mi deporte favorito pueda tener
una buena figura y condición dentro de un año o menos tal vez
Todo esto lo cumpliré
aproximadamente en Agosto de 2018.
Pero debo de vencer la
pereza y esforzarme bien.
Mis principales valores
que estarán presentes serán la responsabilidad, el entusiasmo, el deporte, la
salud e inclusive el auto aceptación.
Como ya mencione
anteriormente debo vencer la pereza, pues esto se trata de dedicación y esfuerzo,
es por ello que tengo que poner empeño en esta meta.
MI
META PRIORITARIA EN EL ASPECTO OCUPACIONAL
ü Mi mayor meta en este aspecto es poder tener una
profesión, no lo he pensado bien pero puede ser contaduría pública o derecho,
dado caso, me gustaría tener un buen trabajo.
En un principio
mencione que yo si realmente quiero tener un trabajo fijo y bien pagado.
Al tener ya un trabajo
como contadora empresarial puedo también trabajar como enseñadora en un centro
educativo de nivel media superior o superior.
Me propuso esta meta
desde ahora y la cumpliré el 22 de Agosto del 2025 posiblemente, si es que no
lo pospongo a más tiempo pero ira dependiendo de la situación que se presente día
a día.
Los principales valores
que tendré serán la perseverancia, la responsabilidad, el respeto, el
compromiso, una buena actitud positiva, el empeño, entre otras.
Venceré todas las
dificultades que tenga con una buena actitud, tal vez en el transcurso de mis
estudios pueda tener ocasiones en las que me quiera rendir, será ahí cuando me
tenga que poner más fuerte y activa.
MI
META PRIORITARIA EN EL ASPECTO ECONOMICO
ü Mi meta
prioritaria es tener un salario bien pagado, con horarios accesibles, una buena
casa, un auto, y ahorros para un futuro próximo.
Me he propuesto mucho
que debo de salir adelante aunque sea sola para poder tener más cosas, para
ayudar a más personas, para brindar gratitud a mi familia, entre otras.
Realmente quiero tener
un buen futuro no solo para mí, si no también para mi pareja futura, mis hijos,
mi familia, y para las demás personas que me rodean, para ello es necesario que
le ponga mucho empeño en cada clase, que cuando consiga ya un trabajo fijo y un
salario bueno, me siga empeñando para obtener más beneficios.
Mi situación económica
quiero que mejore conforme pasen los años, ya que podre vivir tranquilamente, y
me centro mucho en la idea de ayudar a quien más lo necesite. Sé que no lo es
todo pero me empeñare mucho para estar bien en ese aspecto.
Para lograr esto debo
de vencer varios antivalores como son la irresponsabilidad, la desesperación,
la mala comunicación, el estrés, las malas actitudes más que nada
Mi nombre es Yesenia
Flores Romero, soy una joven de 15 años actualmente, actualmente estoy cursando
el primer semestre de preparatoria en el
CBTis 229 y este es mi plan de vida
Una de mis fortalezas
como persona es que soy una buena alumna, durante mis 12 años de preparación
escolar he mostrado un buen comportamiento y buena actitud, ganándome así
varios reconocimientos y aprecio de mis anteriores maestros.
Soy una persona muy
comprensiva, me gusta ayudar. Otra de mis fortalezas que yo poseo es que
aprendo rápido, al igual que no soy conformista, es decir, yo busco muchas más
oportunidades de las que tengo, y hago lo posible por salir adelante a pesar de
cada mala situación que se me presente.
Soy una persona
divertida, y entendible.
Pero no todo es lado positivo
en mí, con esto me refiero es que tengo ciertas debilidades que me perjudican
como persona en el ámbito social y familiar
Una de mis debilidades
es que hay momentos en los que soy muy floja, ya sea para hacer alguna tarea, o
practicar un deporte.
Otra seria que hablo de
mas, oh digo cosas sin sentido perjudicando a terceras personas, al igual que
no soporto comentarios negativos y me tomo las cosas malas muy en serio,
provocando a base de eso que me sienta mal y me dé por vencida.
Otra debilidad que
tengo es que digo malas palabras inclusive en lugares que novan, pero soy
honesta y lo acepto, se oye mal.
Tengo muchos defectos
como cualquier persona pero es ahí cuando debo de portarme más fuerte, más
justa, más responsable y tratar de quitar eso.
Me he puesto a pensar
que si no cambio mi actitud negativa no llegare muy lejos, al contrario, se va
debilitando mis fortalezas, y mis metas se pueden venir abajo con todo lo
propuesto que tengo, así que como ya mencione anteriormente, debo salir
adelante ahora más que nunca.
Me he propuesto a
terminar una carrera, tal vez estudiare Contaduría o Derecho, pero aun no tengo
bien decidido eso, pero lo que sí es seguro es que si conseguiré un título
profesional, podre sacar adelante a mi familia, tener una casa propia, quizá un
auto, un buen trabajo y quizá una familia propia.
Mis principales valores
son los siguientes:
Mi familia: Mi conducta o valor apuesto a esto
es la separación, el egoísmo, la falta de respeto. Esto perjudica mucho nuestra
convivencia y puedo llegar a tener dificultades.
Por lo que
voy hacer todo lo posible por mantener a mi familia unida, tomando una actitud
positiva, obedeciendo, provocando así la mejora de la estabilidad familiar.
Los amigos: Valor opuesto es la enemistad, algo
que hace que las personas se alejen.
Para vencer
esto será necesario ser sincera, apoyarlos, comprender, ser una persona en la
cual se puede confiar, pero es importante saber cómo son el tipo de personas
con las que convivo.
El amor: El valor opuesto al amor es el odio,
provoca la distancia y una mala imagen de mi persona.
Este mal
valor lo venceré dando una buena idea sobre mí, amar a mis personas queridas
como se debe, respetar, confiar, ayudar, entender, querer.
El respeto: Valor opuesto de este es la falta
de respeto, la ignorancia, el egoísmo. Vivimos en una sociedad en la cual este
valor ya no le tiene importancia, al contrario, es el más opacado de todos a
pesar de que es el principal y la base de los demás.
Para poder
vencer todo eso es necesario que yo lo practique para todo, esto incluye en
todos los ámbitos sociales, tomando consideración de este en todas las
personas.
MI
VISION
Lo que yo veo en un
futuro es grande, pues quiero progresar y obtener una buena vida, ya mencione
anteriormente que quiero un buen trabajo, una casa, una familia, un auto quizá.
Quiero tener un buen futuro.
MI
MISION.
Mi misión es lógralo,
lograr mis metas, mis sueños, mis visiones, mis expectativas. Pondré mucho
empeño en las etapas que aún me faltan, para así alcanzar la victoria y
sentirme bien con todo mi esfuerzo.
MI
META EN EL ASPECTO ESPIRITUAL
ü Una meta en
el aspecto espiritual es seguir siendo creyente de una religión o inclusive
poder hacer un servicio a la comunidad religiosa, es decir, ser misionera, ser
lectora o esas cosas.
ü Otra podría
ser alimentar mi espíritu haciendo alguna actividad tranquila; practicar yoga
tal vez, todo estopara mantenerme tranquila conmigo misma.
En el primer aspecto no
lo tengo del todo bien definido ya que hay veces en las que no soy tan
creyente.
Pero me propongo hacer
el intento para hacer algún servicio religioso.
Esto lo lograre
aproximadamente el 15 de Enero de 2018, tendrá beneficios para la sociedad
espiritual y también para mí.
Pero vuelvo a repetir
nuevamente, esto no es nada seguro dependiendo de mis creencias que tenga
posteriormente, pero respetare la de los demás alejándome de críticas o
prejuicios.
Esto lo lograre
evitando los malos comentarios, tomando el valor de respeto como el principal y
dejar los prejuicios de un lado, además de la paz interior en mí.
MI
META PRIORITARIA EN EL ASPECTO
INTELECTUAL
Una de mis metas en
este aspecto es:
ü Terminar una
profesión, ya mencionado anteriormente aun no tengo bien definido qué carrera elegiré,
pero dado caso que sea contaduría, es necesario saber cómo lo hare, es por ello
que lo describo a continuación.
Al terminar mis
estudios universitarios buscare un trabajo, ya sea como ayudante en un despacho
contable, para iniciar así una pequeña practica para después poder conseguir
uno mejor pagado ya sea en una empresa grande o como contadora privada de
distintas personas, pues he escuchado que es un buen trabajo.
Estamos a 19 de
septiembre de 2017, para el día 20 de Septiembre de 2024 ya estaré consiguiendo
algún trabajo como auxiliar contable aproximadamente. Sera hasta 1 o 2 años muy
máximos ya poder contar con un trabajo estable en una empresa.
Tendré un buen sueldo,
y podre empezar ahorrar para mis gastos posteriores que tenga
Seré reconocida como
una buena contadora y solicitada por varios clientes, logrando así otro merito
ganado
Los valores que tendré
para logar esto serán la perseverancia, su mala actitud de este es rendirse,
pues como dicen ``El que persevera alcanza``
Otro valor será el
respeto, como ya mencione anteriormente, es la base de todo.
El conocimiento, al
igual que la responsabilidad, pues ser contador no es nada fácil
Todos los valores no se
verán opacados si tomo iniciativa y buena actitud de mi parte.
MI
META PRIORITARIA EN EL ASPECTO AFECTIVO/ EMOCIONAL
ü Mi meta
prioritaria en este aspecto es poder formar una familia y casarme al concluir
mis estudios universitarios, posteriormente formar una familia, seguir teniendo
buenas compañías.
Para esto será
necesario de una vez pensar en lo que hare.
Al terminar mis
estudios o mi carrera, buscare un trabajo como ya mencione anteriormente, ya
que tenga todo esto decidiré por encontrar una buena persona con la cual
compartir lo que resta de mi vida.
20 de septiembre de
2017, estoy cursando el primer semestre de nivel media superior, será hasta el día
22 de Diciembre de 2027 aproximadamente cuando me casare, pero todo esto depende
de lo que pueda pasar posteriormente, ya que no es fácil encontrar una buena
persona que comparta gustos en común.
Antes de la unión
matrimonial, comenzare a ahorrar junto a mi pareja para los preparativos, para
poder empezar a construir una vivienda y para tener recursos con los cuales
poder vivir bien.
Ya que tengamos todo
esto tal vez tengamos 2 hijos, estos les brindaremos todos los recursos
necesarios para su sano crecimiento.
Viviremos bien, ya que
ambos nos apoyaremos mutuamente.
Mi
principal valor para logara esto será el amor, la comprensión, y la unión.
Tendremos antivalores como son el odio, la separación. Para poder combatir esto
debo dar lo mejor de mí y apoyare a mi
familia y pareja en lo que pueda, siempre cuidándolos y dándonos ánimos para
cada situación difícil.
MI META PRIORITARIA EN EL ASPECTO FAMILIAR
MI META PRIORITARIA EN EL ASPECTO FAMILIAR
ü Una de mis
metas prioritarias en el aspecto familiar es poder brindarles a mi familia
actual más recursos, terminar su casa, darles más atención y poder
fortalecernos.
Esto no será nada
sencillo, pues todo esto depende de que yo consiga un buen trabajo. Para poder
regresarles todo el esfuerzo que han hecho por mis durante mis primeros años de
preparación escolar.
Si empiezo a trabajar
desde ahora 25 de septiembre de 2017, y ahorrar más y más, no solo para mis
estudios sino también para ayudar a mi familia, a más tardar el 25 de Enero del
2022 empezare con terminar mi casa.
Después de esto, al
obtener un buen salario empresarial le daré a mis padres un descanso, darles más
recursos médicos y ocuparme de darles varias atenciones.
Mis principales valores
para lograr esto serán la familia, la perseverancia, la unión, el amor.
Alguna de las malas
actitudes que pueda haber, puede ser la falta de comunicación entre familia, ya
que puede ocasionar muchos conflictos, pero para ello, no debo enojarme ni
desobedecer, si no hacer que la convivencia mejore junto a ella el cariño.
MI
META PRIORITARIA EN EL ASPECTO RECREATIVO
ü En este
aspecto mi principal meta es poder divertirme de una manera sana, a que me
refiero con esto, que mi deporte favorito es el futbol, por ello una buena
manera de divertirme es pertenecer a un equipo femenil de futbol por un tiempo,
o inclusivamente, cuando tenga mi familia poder jugar con ellos.
Actualmente no practico
el deporte por la falta de tiempo e igual de recursos, pero si me sigo
esforzando como lo he estado haciendo, empezare mis entrenamientos el próximo
semestre.
Ya que empiece desde
cero a practicar lo más probable es que aproximadamente 22 de Enero de 2019 ya estaré
más preparada en este deporte.
Pero podre divertirme
al practicar en cada sesión deportiva de una manera sana, mas sin embargo si me
gustaría poder participar en un equipo femenil.
Los valores para poder
llevar a cabo esto serán la diversión sana, el deporte, la responsabilidad, el
entusiasmo, la perseverancia.
Algunos de ellos se
verán opacados por la irresponsabilidad, el cansancio, el estrés, o quizá la
falta de compromiso, por ello, debo de pensar bien las cosas antes de
realizarlas, por lo que me comprometeré a echarle ganas, divertirme bien por
supuesto, ser activa y respetuosa.
Al concentrarme en mi y
en mi integridad física, esta es una buena manera de divertirse y no solo salir
con amigos a un antro o disco, pues nos exponemos más a las malas influencias
vicios.
MI
META PRIORITARIA EN EL ASPECTO SOCIAL
ü Mi meta
prioritaria en este aspecto es poder seguir teniendo una buena convivencia con
amigos, familiares y entre toda la sociedad.
ü Otra meta
prioritaria es poder ayudar a la sociedad de hoy en día en diferentes factores,
pues hemos pasado por situaciones difíciles que sería bueno brindar apoyo a los
más necesitados, por ello quiero ya sea poder donar víveres, brindar ayuda personal,
haciendo servicios sociales, entre otros.
Quiero tener buenas
compañías durante toda mi vida, seguir conviviendo con anteriores compañeros
que comparten algunos gustos comunes conmigo, al igual que poder tener una
buena relación con mi pareja, con mis familiares y diferentes personas que me
rodean.
En un futuro tal vez me
anime a ser rescatista, o tener la oportunidad de donar diferentes artículos.
También me gustaría
crear muchas campañas que concienticen a las personas sobre la contaminación
del planeta, ya que por la ignorancia no se han dado cuenta de los daños que
nosotros mismos le ocasionamos
Mis valores que tendré
presente durante este reto será la solidaridad, el respeto, la unión, la paz,
la equidad para todos.
Debo combatir todos los
prejuicios que la sociedad ha de tener, y esquivar algunas barreras que quizá
el mundo político forme.
MI
META PRIORITARIA EN EL ASPECTO CORPORAL
ü Mi meta que
tengo para este aspecto, tal vez pueda sonar muy soberbio, pero me gustaría
ejercitarme teniendo así una vida sana y una buena figura, al igual que una
excelente condición física.
Si empiezo a
ejercitarme correctamente desde esta semana, será el día 25 de septiembre de
2017, posiblemente alcance una mayor rendición en 3 o 4 meses después, es
decir, esto sería por Diciembre o Enero de 2018.
Si continúo
ejercitándome día a día, sanamente, y practicar mi deporte favorito pueda tener
una buena figura y condición dentro de un año o menos tal vez
Todo esto lo cumpliré
aproximadamente en Agosto de 2018.
Pero debo de vencer la
pereza y esforzarme bien.
Mis principales valores
que estarán presentes serán la responsabilidad, el entusiasmo, el deporte, la
salud e inclusive el auto aceptación.
Como ya mencione
anteriormente debo vencer la pereza, pues esto se trata de dedicación y esfuerzo,
es por ello que tengo que poner empeño en esta meta.
MI
META PRIORITARIA EN EL ASPECTO OCUPACIONAL
ü Mi mayor meta en este aspecto es poder tener una
profesión, no lo he pensado bien pero puede ser contaduría pública o derecho,
dado caso, me gustaría tener un buen trabajo.
En un principio
mencione que yo si realmente quiero tener un trabajo fijo y bien pagado.
Al tener ya un trabajo
como contadora empresarial puedo también trabajar como enseñadora en un centro
educativo de nivel media superior o superior.
Me propuso esta meta
desde ahora y la cumpliré el 22 de Agosto del 2025 posiblemente, si es que no
lo pospongo a más tiempo pero ira dependiendo de la situación que se presente día
a día.
Los principales valores
que tendré serán la perseverancia, la responsabilidad, el respeto, el
compromiso, una buena actitud positiva, el empeño, entre otras.
Venceré todas las
dificultades que tenga con una buena actitud, tal vez en el transcurso de mis
estudios pueda tener ocasiones en las que me quiera rendir, será ahí cuando me
tenga que poner más fuerte y activa.
MI
META PRIORITARIA EN EL ASPECTO ECONOMICO
ü Mi meta
prioritaria es tener un salario bien pagado, con horarios accesibles, una buena
casa, un auto, y ahorros para un futuro próximo.
Me he propuesto mucho
que debo de salir adelante aunque sea sola para poder tener más cosas, para
ayudar a más personas, para brindar gratitud a mi familia, entre otras.
Realmente quiero tener
un buen futuro no solo para mí, si no también para mi pareja futura, mis hijos,
mi familia, y para las demás personas que me rodean, para ello es necesario que
le ponga mucho empeño en cada clase, que cuando consiga ya un trabajo fijo y un
salario bueno, me siga empeñando para obtener más beneficios.
Mi situación económica
quiero que mejore conforme pasen los años, ya que podre vivir tranquilamente, y
me centro mucho en la idea de ayudar a quien más lo necesite. Sé que no lo es
todo pero me empeñare mucho para estar bien en ese aspecto.
Para lograr esto debo
de vencer varios antivalores como son la irresponsabilidad, la desesperación,
la mala comunicación, el estrés, las malas actitudes más que nada
Comentarios
Publicar un comentario